Parallel computation thesis
In computational complexity theory, the parallel computation thesis is a hypothesis which states that the time used by a (reasonable) parallel machine is polynomially related to the space used by a sequential machine. The parallel computation thesis was set forth by Chandra and Stockmeyer in 1976 (see References).
In other words, for a computational model which allows computations to branch and run in parallel without bound, a formal language which is decidable under the model using no more than 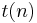 steps for inputs of length n is decidable by a machine in the unbranching model using no more than
steps for inputs of length n is decidable by a machine in the unbranching model using no more than 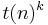 units of storage for some constant k. Similarly, if a machine in the unbranching model decides a language using no more than
units of storage for some constant k. Similarly, if a machine in the unbranching model decides a language using no more than 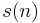 storage, a machine in the parallel model can decide the language in no more than
storage, a machine in the parallel model can decide the language in no more than 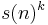 steps for some constant k.
steps for some constant k.
The parallel computation thesis is not a rigorous formal statement, as it does not clearly define what constitutes an acceptable parallel model. A parallel machine must be sufficiently powerful to emulate the sequential machine in time polynomially related to the sequential space; compare Turing machine, non-deterministic Turing machine, and alternating Turing machine. N. Blum (1983) has introduced a model for which the thesis does not hold. However, the model allows 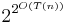 parallel threads of computation after
parallel threads of computation after 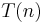 steps. (See Big O notation.) Parberry (1986) suggested a more "reasonable" bound would be
steps. (See Big O notation.) Parberry (1986) suggested a more "reasonable" bound would be 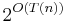 or
or 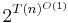 , in defense of the thesis. Goldschlager (1982) has proposed a model which is sufficiently universal to emulate all "reasonable" parallel models, which adheres to the thesis. Chandra and Stockmeyer originally formalized and proved results related to the thesis for deterministic and alternating Turing machines, which is where the thesis originated.
, in defense of the thesis. Goldschlager (1982) has proposed a model which is sufficiently universal to emulate all "reasonable" parallel models, which adheres to the thesis. Chandra and Stockmeyer originally formalized and proved results related to the thesis for deterministic and alternating Turing machines, which is where the thesis originated.
References
- Blum, N., "A note on the 'parallel computation thesis'," Inf. Proc. Lett., volume 17, pp. 203-205, 1983.
- Chandra, A.K. and Stockmeyer, L.J., 'Alternation,' Journal of the ACM, Volume 28, Issue 1, pp. 114-133, 1981.
- Goldschlager, Leslie M., 'A Universal Interconnection Pattern for Parallel Computers,' Journal of the ACM, Volume 29, Issue 3, pp. 1073-1086, 1982.
- Parberry, I., 'Parallel speedup of sequential machines: a defense of parallel computation thesis,' ACM SIGACT News, Volume 18, Issue 1, pp. 54-67, 1986.